Binh Ho
Are random seeds hyperparameters?
In many types of programming, random seeds are used to make computational results reproducible by generating a known set of random numbers. However, the choice of a random seed can affect results in non-trivial ways.
Here, I’ll cover a discussion around whether the random seed should be treated as a hyperparameter in machine learning. That is, should we “optimize” the random seed to get the best results possible? This seems like a silly idea upfront — trying to optimize something that is intended to be unrelated to the model’s results — but there is already precedent for doing this in some areas of machine learning.
In most situations, the random seed can be set without much thought. I was amused by this graph generated by Jake VanderPlas showing the most common seed values:
The frequency of random seeds between 0 and 1000 on github (data from https://t.co/xwutMzNI2N) pic.twitter.com/Zmp7mwMWil
— Jake VanderPlas (@jakevdp) April 8, 2020
However, in machine learning (and specifically deep learning), it is becoming clear that the choice of random seed can have a large effect on one’s code and one’s ultimate computational results. There has been a debate about how exactly we should think of the random seed: should we treat it as a legitimate hyperparameter, or should we be skeptical of results that depend on the random seed?
I first learned about this debate from a tweet by Prof. Dan Roy (where SOTA means “state of the art”):
Your SOTA code may only be SOTA for some random seeds. Nonsense or new reality? I suppose there are trivial ways to close the gap using restarts and validation data.https://t.co/nhuJrOlqgs pic.twitter.com/mzRGLGH4ZV
— Daniel Roy (@roydanroy) April 15, 2020
In the paper Roy referenced, the authors tried to quantify how much their results changed on an NLP task depending on the choice of the initial random seed. The first line of the abstract is
Fine-tuning pretrained contextual word embedding models to supervised downstream tasks has become commonplace in natural language processing. This process, however, is often brittle: even with the same hyperparameter values, distinct random seeds can lead to substantially different results.
In their results, they found that the random seed does indeed affect their results, often in very significant ways:
Further, we examine two factors influenced by the choice of random seed: weight initialization and training data order. We find that both contribute comparably to the variance of out-of-sample performance, and that some weight initializations perform well across all tasks explored.
So, if the random seed can have a large effect on downstream results, should we be tuning the random seed as if it were a hyperparameter, and report these seeds and their generators?
Background on random seeds
Computers don’t generate truly random numbers. Instead, they generate pseudorandom numbers using pseudorandom number generators. Different programming languages and computer architectures have varying types of these generators, but the basic idea is the same: the user gives the generator a “random seed” (which is just a number), and given that seed, the generator generates out a sequence of numbers that follow some probability distribution.
However, given a random seed, this sequence of numbers is always the same. In a way, once the seed is set, the numbers are no longer “random” in some sense. For example, consider numpy’s pseudorandom generator. If we set the seed to be 1, generate 5 numbers, then reset the seed, and generate another 5 numbers, this sequence of numbers will be the same each time.
You can verify this for yourself with the following code:
import numpy as np
# Trial 1
np.random.seed(1)
x1 = np.array([np.random.uniform() for _ in range(5)])
# Trial 2
np.random.seed(1)
x2 = np.array([np.random.uniform() for _ in range(5)])
# Check if same
print(np.array_equal(x1, x2)) # should return True
Mechanisms for the random seed’s influence
It seems clear empirically that the random seed can significantly affect model performance. But how exactly does the random seed influence the results?
In essence, any piece of code that is dependent on the random seed is subject to possibly changing the model’s performance. The main attributes that are typically determined by random seeds are
- Initial values of the model’s parameters before training
- Which data samples appear in the training set vs. the test set
- The order in which the training samples are presented to the model
These are also the attributes studied by Dodge et al.
We’ll step through these one-by-one to show a more detailed picture of how the random seed affects each of these, which in turn affects model performance.
Initial values of model parameters
In many learning settings that use gradient descent – or another type of iterative learning – it’s common to set the initial values of the parameters randomly. These initial values are directly determined by the random seed.
For example, suppose we have the following objective function that we’d like to minimize:
\[f(x) = 0.01x^6 + (x-0.2)^3 + 2(x-1)^2.\]Here’s a plot of the function:
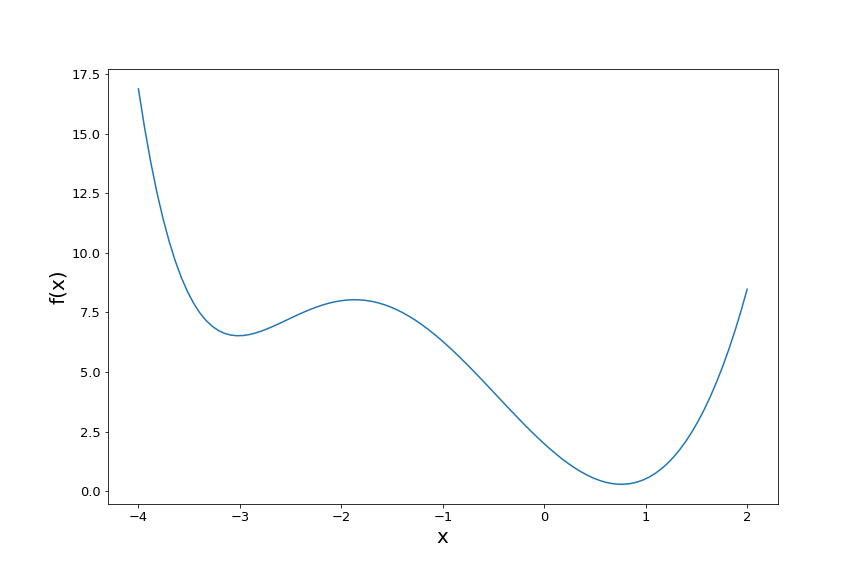
It has two local minima. Now, say our ultimate goal is to find the global minimum (the one on the right) using gradient descent. Clearly, our initial starting value before starting gradient descent will have a large influence on which minimum we end up in.
Indeed, let’s try running gradient descent with two different initial random seeds — 8 and 9 — with the following code. (Here, we assume we have perfect gradient information, which is unrealistic in most situations, but it works for illustrative purposes.)
import numpy as np
def f(x):
return 0.01*x**6 + (x-0.2)**3 + 2*(x-1)**2
def grad_f(x):
return .06*x**5 + 3*(x-0.2)**2 + 4*(x-1)
x1, x2 = -4, 2
xs = np.linspace(x1, x2, 100)
## RANDOM SEED = 8
np.random.seed(8)
# Get initial value
x0 = np.random.uniform(x1, x2, size=1)
est = x0.copy()
# Gradient descent
for _ in range(100):
est -= 0.01 * grad_f(est)
plt.figure(figsize=(24, 8))
plt.subplot(121)
plt.plot(xs, f(xs), c='black')
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("np.random.seed(8)")
# Plot initial value and final value
col = 'red' if est < -1 else 'blue'
plt.scatter(est, f(est), c=col)
plt.axvline(x0, ymax = 0.03, c=col)
## RANDOM SEED = 9
np.random.seed(9)
# Get initial value
x0 = np.random.uniform(x1, x2, size=1)
est = x0.copy()
# Gradient descent
for _ in range(100):
est -= 0.01 * grad_f(est)
plt.subplot(122)
plt.plot(xs, f(xs), c='black')
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("np.random.seed(9)")
# Plot initial value and final value
col = 'red' if est < -1 else 'blue'
plt.scatter(est, f(est), c=col)
plt.axvline(x0, ymax = 0.03, c=col)
We see that these seeds end up in different minima, with 8 finding the global minimum, and 9 getting stuck in the other local minimum. Here’s a plot showing each initial value as the tick mark at the bottom, and the final value after gradient descent as a dot on the function plot.
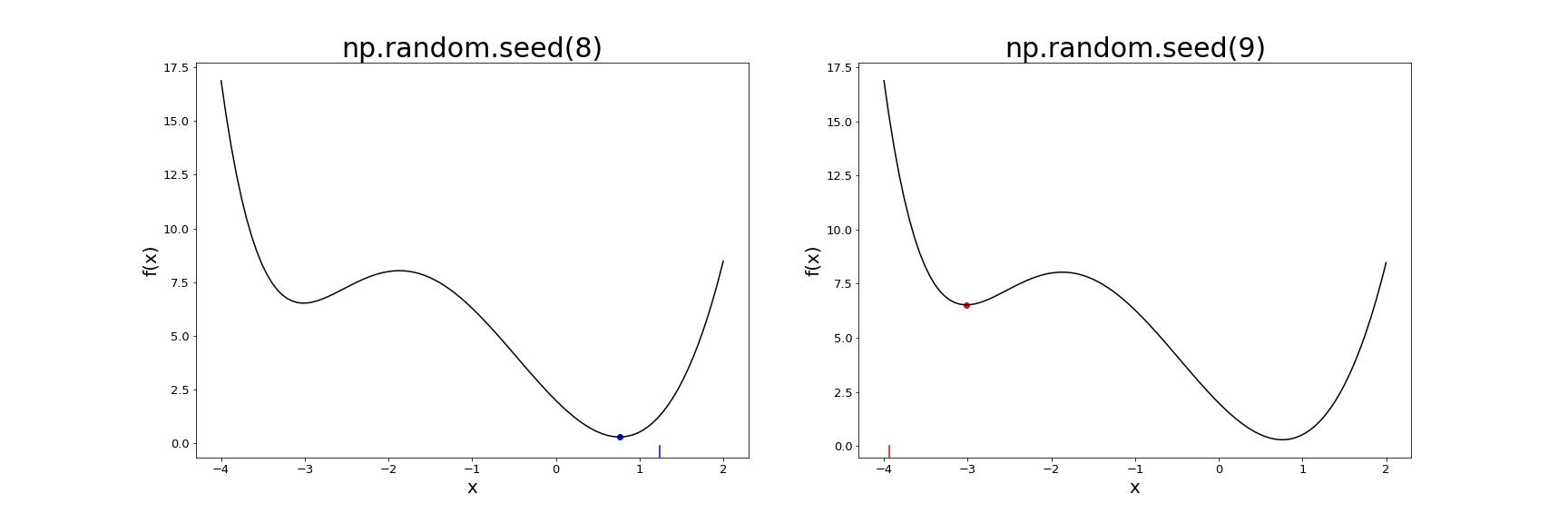
Train/test split
The way that the random seed affects model performance via the split between train and test data is a bit more straightforward. At its core, it depends on whether the data in the train split is representative of the whole population of data. If you fit a model on an outlier subset of data, then the model will likely perform poorly on the test data.
To make this more concrete, let’s consider the setting of simple linear regression. Let’s say we have 100 total data points, and we fit the model on 75 of them. We can choose these 75 points randomly, by first setting a random seed.
Let’s say we fit the linear model 10 times, using random seeds 1 through 10. This can be done with the following code:
from sklearn.metrics import r2_score
train_frac = 0.75
n_train = int(train_frac * n)
r2s = []
for ii in range(1, 11):
# Set seed
np.random.seed(ii)
# Train/test split
train_idx = np.random.choice(np.arange(n), size=n_train)
test_idx = np.setdiff1d(np.arange(n), train_idx)
X_train = X[train_idx]
X_test = X[test_idx]
y_train = y[train_idx]
y_test = y[test_idx]
# Estimate beta and test
ols_est = np.dot(X_train, y_train) / np.dot(X_train, X_train)
yhat_test = ols_est * X_test
r2s.append(r2_score(yhat_test, y_test))
We can see that the $R^2$ of the fit on the test data varies fairly substantially depending on the random seed.
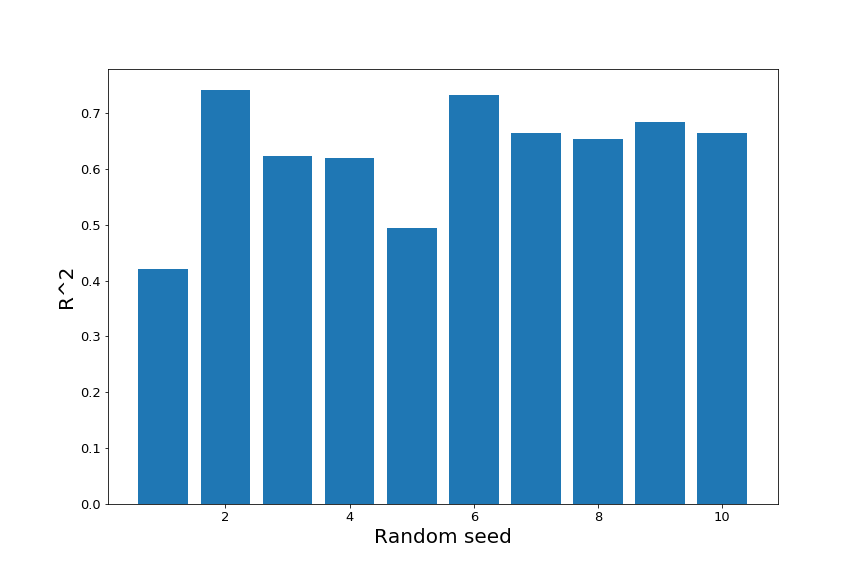
Conclusion
It’s undeniable that the random seed has a substantive effect on model results in many learning situations. However, it’s up for debate how we should think of random seeds, and if/how we should report random seeds in the literature.
Some models’ dependence on randomness has been known for quite a while (e.g., doing random restarts with certain algorithms, like k-means). However, if certain random seeds are known to perform better with some types of algorithms on certain datasets, this seems worth reporting in a consistent manner. This is even more true when fitting these models is expensive in terms of time, money, and electricity (this is particularly true in deep learning).
The random seed debate could be another point in favor of deep learning being alchemy, or a simple reality about algorithms that depend on randomness. Either way, the empirical effect of random seeds is clear.
References
- Dodge, Jesse, et al. “Fine-tuning pretrained language models: Weight initializations, data orders, and early stopping.” arXiv preprint arXiv:2002.06305 (2020).